Manipulando Dados com Grafos
Bernardo Fontes
São Paulo/SP
13 de Dezembro de 2018
## WARNING!
- ### O Teoria de Grafos é uma **área inteira** em Ciência da Computação
- ### Veremos algumas partes dela nessa palestra para avaliarmos a **utilidade** do tema
- ### Encorajo muito a buscarem mais informações e trocarmos ideia depois da palestra
## Roteiro
- O que são grafos?
- Possíveis análises
- Persistindo no banco
- Exemplos no mundo real
## O que são grafos?
- Estrutura composta por **nós e arestas**
- **Nós** possuem dados
- **Arestas** definem relações entre os nós
- As relações são entidades, ou seja, podem **possuir dados** também
Exemplo clássico
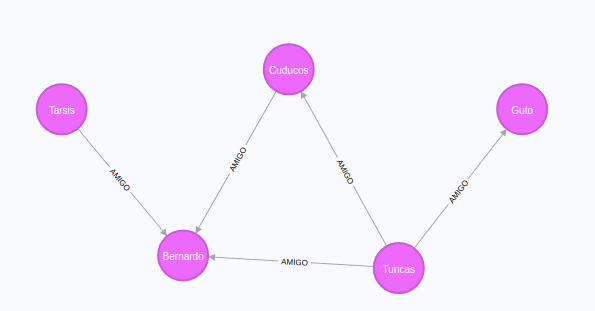## Quando usar grafos?
- Quando o *domínio do problema* e/ou *entendimento dos dados* é muito mais atrelado a **como as entidades se relacionam** do que com suas mudanças de estado
Exemplo mais real
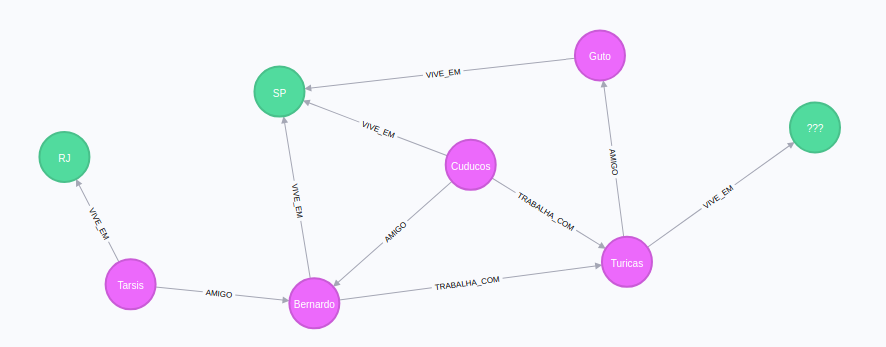## Quais tecnologias usar?
- Análise: Python + **networkx**
- Persistência: Neo4j
## Possíveis análises
- Centralidades
- Clusterização
- Percursos no grafo
- Padrões estruturais da rede
- E por aí vai...
## Centralidades
- Degree
- Closeness
- Betweenness
- Eigenvector
- Existem outras
Nosso grafo
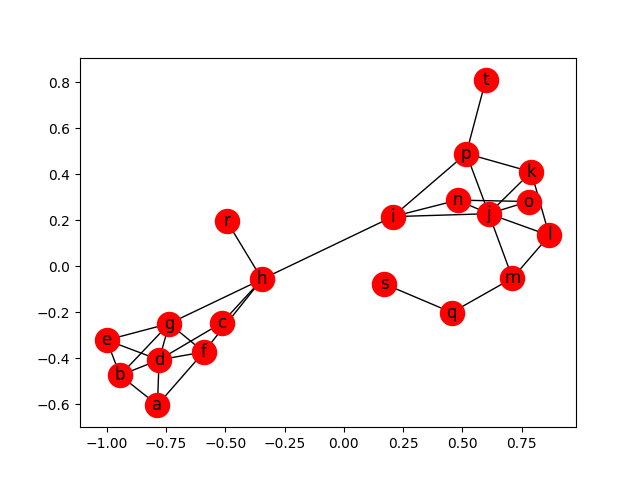## Input de texto
```
sq
ml
mj
mq
lk
lj
...
```
## Criando o grafo
```python
import networkx as nx
def get_graph():
graph = nx.Graph()
with open('links.txt', 'r') as fd:
lines = fd.readlines()
for line in lines:
node_1, node_2 = line.strip()
graph.add_edge(node_1, node_2)
return graph
```
## Degree centrality
- Centralidade baseada diretamente no número de arestas de um nó
## Degree centrality
```python
g = get_graph()
centralities = nx.degree_centrality(g)
centralities = sorted(centralities.items(), key=lambda x: x[1], reverse=True)
for node, value in centralities:
print('{} - {}'.format(node, value))
```
## Degree centrality - Resultado
```
j - 0.3684210526315789
d - 0.3157894736842105
h - 0.2631578947368421
g - 0.2631578947368421
p - 0.21052631578947367
i - 0.21052631578947367
f - 0.21052631578947367
b - 0.21052631578947367
m - 0.15789473684210525
l - 0.15789473684210525
k - 0.15789473684210525
n - 0.15789473684210525
a - 0.15789473684210525
e - 0.15789473684210525
q - 0.10526315789473684
o - 0.10526315789473684
c - 0.10526315789473684
s - 0.05263157894736842
t - 0.05263157894736842
r - 0.05263157894736842
```
Degree centrality - Resultado
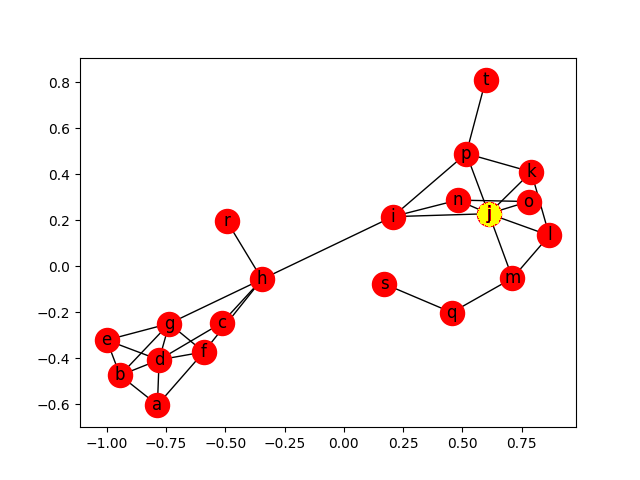
Útil para análises quantitativas totais
## Closeness centrality
- Centralidade baseada na distância entre os nós
## Closeness centrality
```python
g = get_graph()
centralities = nx.closeness_centrality(g)
centralities = sorted(centralities.items(), key=lambda x: x[1], reverse=True)
for node, value in centralities:
print('{} - {}'.format(node, value))
```
## Closeness centrality - Resultado
```
i - 0.4634146341463415
h - 0.4418604651162791
j - 0.4318181818181818
p - 0.3877551020408163
n - 0.37254901960784315
g - 0.3584905660377358
f - 0.35185185185185186
c - 0.3392857142857143
m - 0.3333333333333333
l - 0.3275862068965517
k - 0.3220338983050847
o - 0.3114754098360656
r - 0.3114754098360656
d - 0.296875
b - 0.2878787878787879
t - 0.2835820895522388
a - 0.2835820895522388
e - 0.2835820895522388
q - 0.2602739726027397
s - 0.2087912087912088
```
Closeness centrality - Resultado
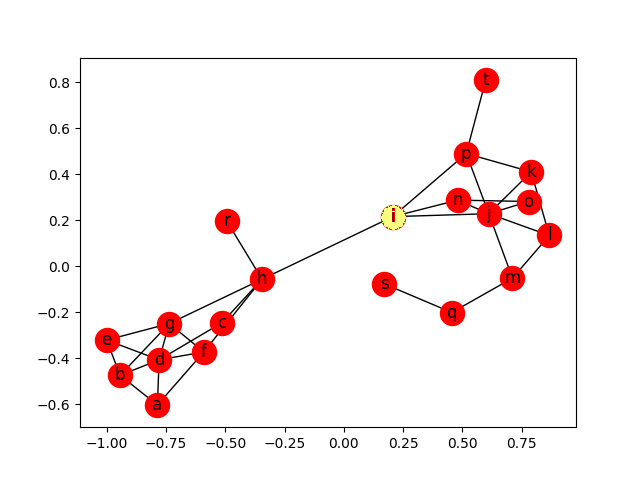
Útil para análises com o objetivo de otimizar propagações
## Betweenness centrality
- Centralidade baseada em caminhos ao qual o nó pertence como intermediário
## Betweenness centrality
```python
g = get_graph()
centralities = nx.betweenness_centrality(g)
centralities = sorted(centralities.items(), key=lambda x: x[1], reverse=True)
for node, value in centralities:
print('{} - {}'.format(node, value))
```
## Betweenness centrality - Resultado
```
h - 0.5614035087719298
i - 0.5321637426900585
j - 0.41812865497076024
m - 0.19883040935672514
g - 0.18226120857699804
p - 0.13450292397660818
q - 0.10526315789473684
f - 0.1033138401559454
d - 0.03313840155945419
n - 0.029239766081871343
c - 0.025341130604288498
l - 0.008771929824561403
k - 0.005847953216374269
b - 0.004873294346978557
a - 0.001949317738791423
s - 0.0
t - 0.0
o - 0.0
r - 0.0
e - 0.0
```
Betweenness centrality - Resultado
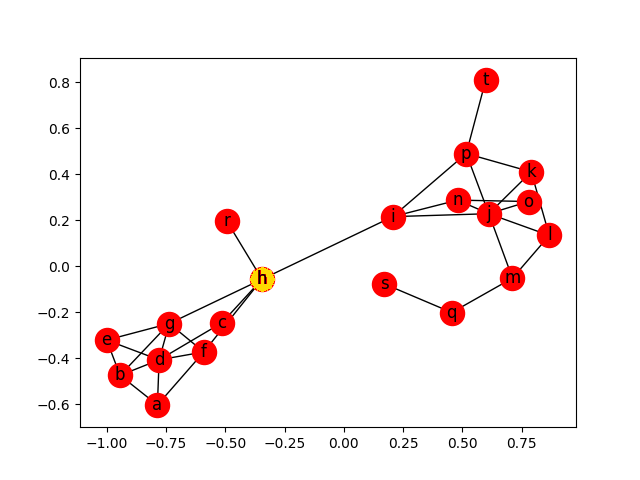
Útil para identificações pontos de entradas de clusters
## Eigenvector centrality
- Centralidade baseada na influência de um nó na rede (topologia)
## Eigenvector centrality
```python
g = get_graph()
centralities = nx.eigenvector_centrality(g, max_iters=1000)
centralities = sorted(centralities.items(), key=lambda x: x[1], reverse=True)
for node, value in centralities:
print('{} - {}'.format(node, value))
```
## Eigenvector centrality - Resultado
```
d - 0.4624402711011163
g - 0.426845473522682
b - 0.3581392113941398
f - 0.3534627131011391
e - 0.30255496341693877
a - 0.2847564509725969
h - 0.28327303565327666
c - 0.18086819094144457
i - 0.1380402866193515
j - 0.12545874636983892
p - 0.08464539539539807
n - 0.07574895588735901
r - 0.06870626212854221
k - 0.06495072621439604
l - 0.05767676369108016
o - 0.04880319165681279
m - 0.0473817168614392
t - 0.020530832833996485
q - 0.012210983147939322
s - 0.0029618234810396492
```
Eigenvector centrality - Resultado
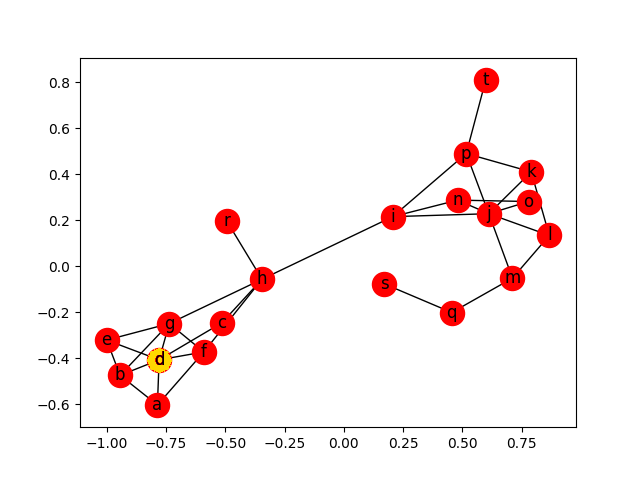
Versões iniciais do PageRank do Google
## Persistência
- Neo4j
- BD Orientado a Grafos escrito em **Java**
- **Cypher** query language == SQL do Neo4j
- **Bolt** é o protocolo de comunicação utilizado
- Módulo **py2neo** para comunicação com o banco
Interface web
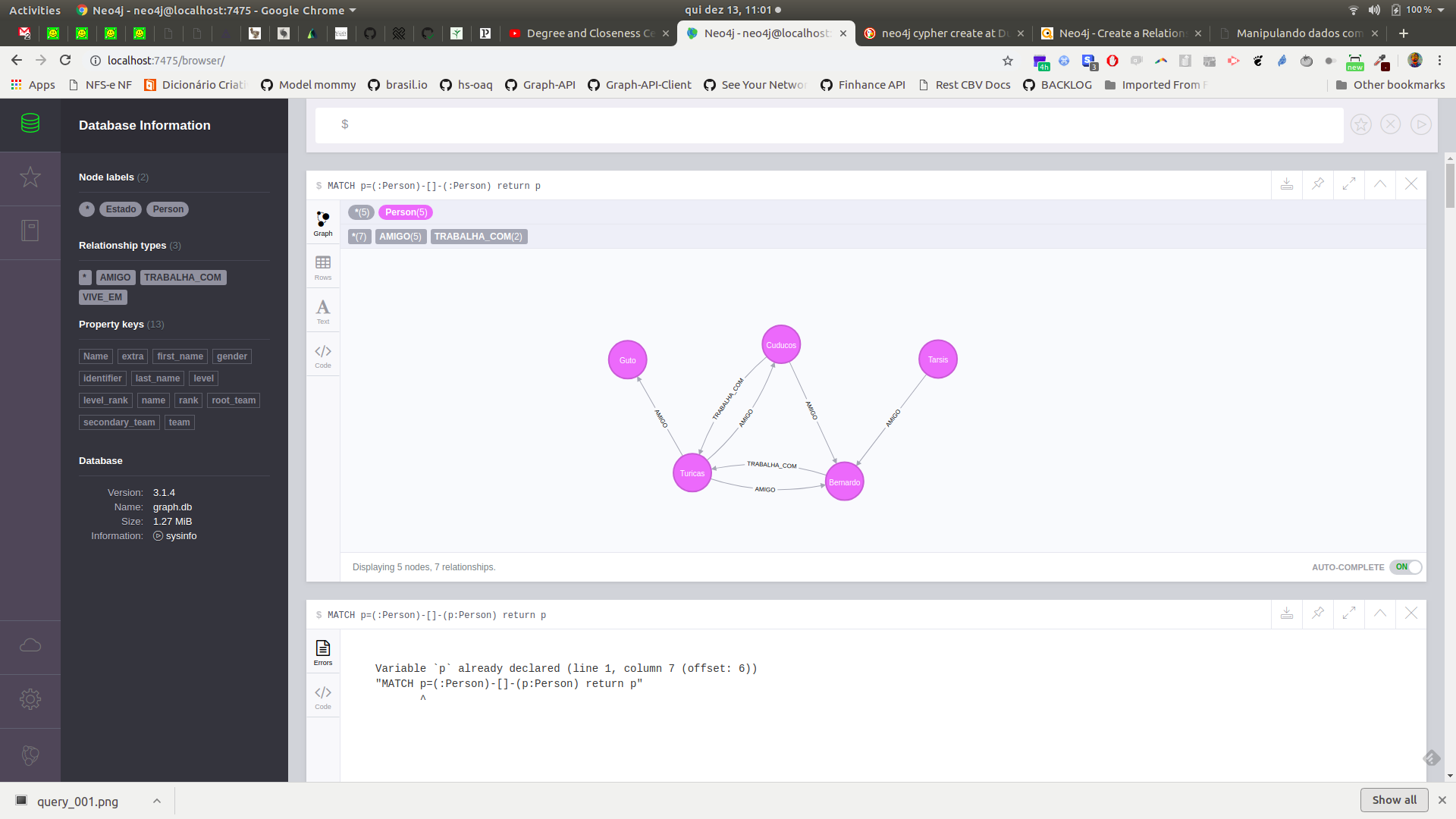
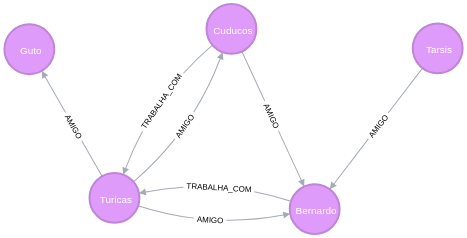
Voltando ao nosso exemplo
Recuperando o grafo de pessoas via Cypher
MATCH
p=(:Person)-[]->(:Person)
RETURN p;
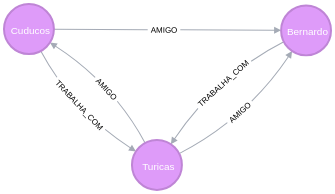
Grafo de pessoas que trabalham juntas
MATCH
p=(:Person)-[:TRABALHA_COM]-(:Person)
RETURN p;
Grafo das pessoas que moram em SP
MATCH
p=(:Person)-[]->(state:Estado)
WHERE
state.Name='SP'
RETURN p;
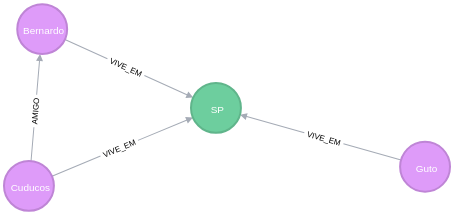
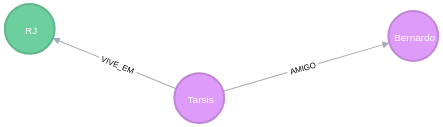
Grafo das pessoas amigas de pessoas que moram no RJ
MATCH
p=(:Person)-[:AMIGO]-(:Person)-[:VIVE_EM]-(state:Estado)
WHERE
state.Name='RJ'
RETURN p;
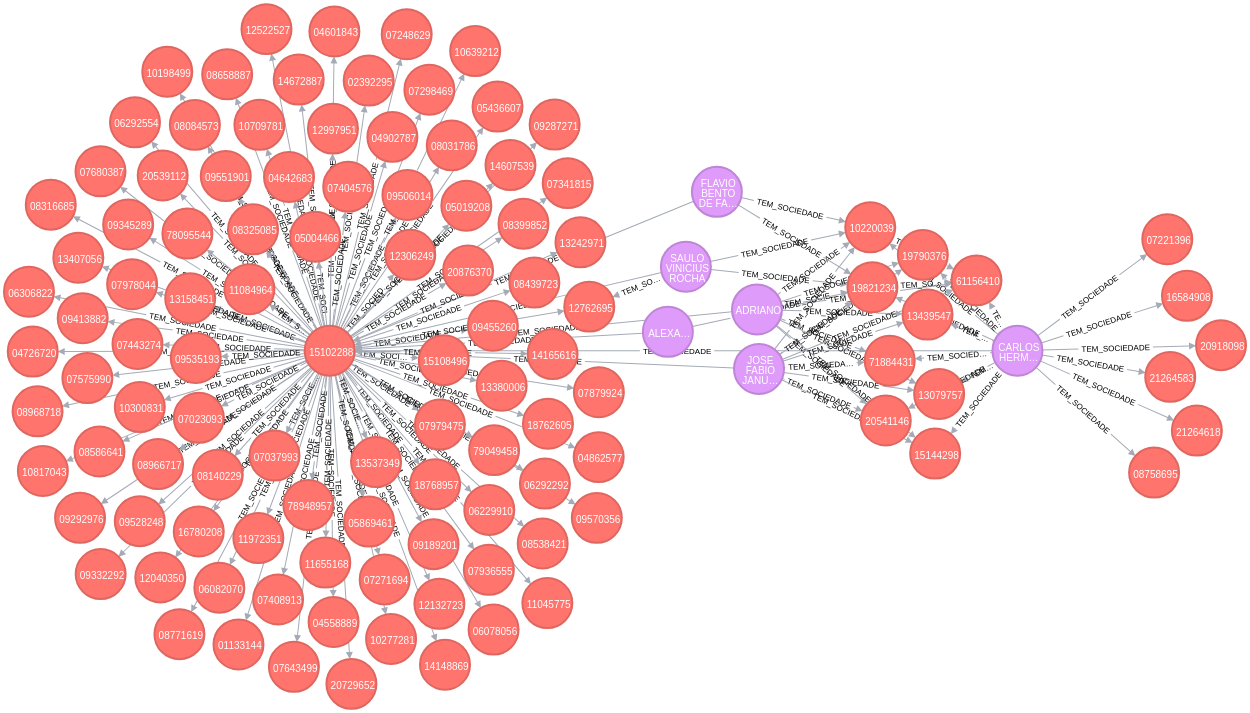
Exemplo real: Brasil.io
Exemplo real: Jazz anos 60
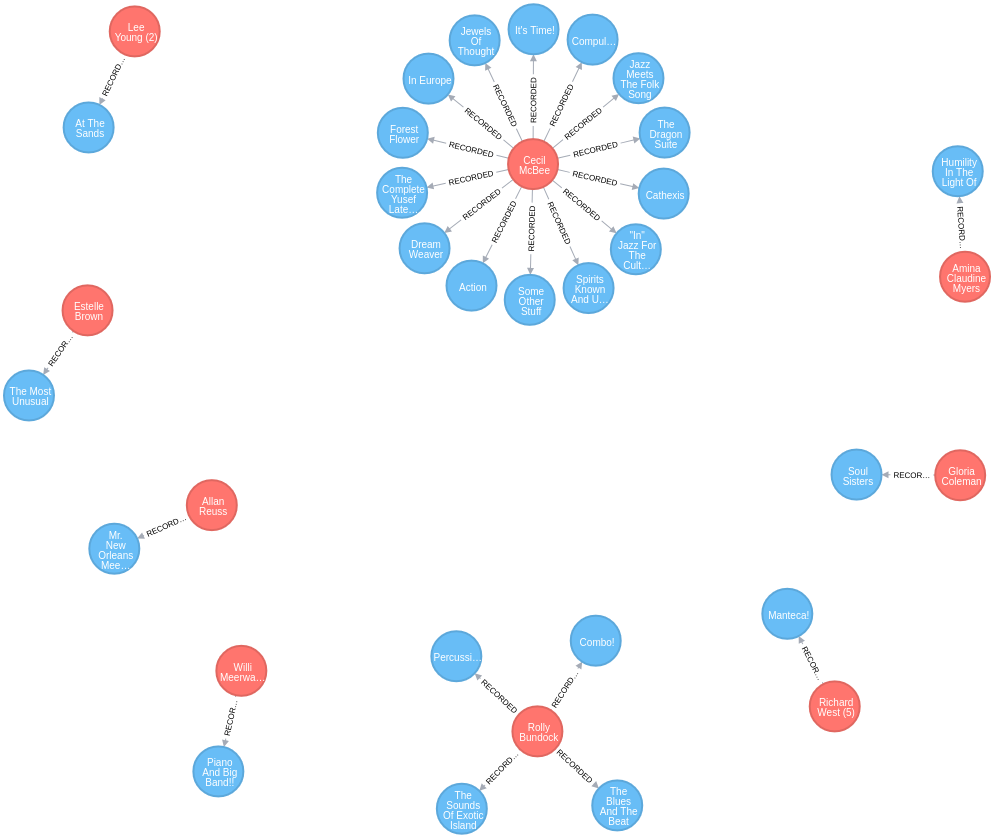
Exemplo real: Jazz anos 60
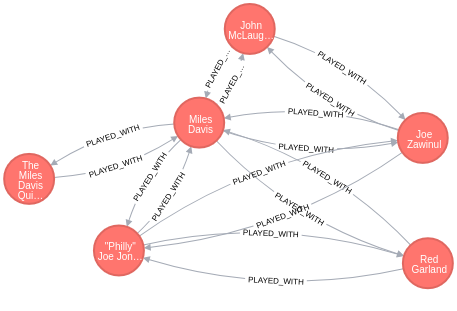
Grafos e uma Análise Matemática do Jazz nos anos 60
## Conclusões
- O módulo do **networkx** já tem 99% do que você precisa
- NoSQL **não** é uma estratégia para todos os problemas
- Saiba quais **perguntas** fazer e quais **métricas** as respondem
- Não confie em apenas uma métrica
